ML lec 03 - Linear Regression의 cost 최소화 알고리즘의 원리 설명
2021. 5. 23. 17:29
출처 : 모두를 위한 머신러닝/딥러닝 https://hunkim.github.io/ml/
모두를 위한 머신러닝/딥러닝 강의
hunkim.github.io

간단하게 표현하기 위해 hypothesis에서 b를 삭제하고 H(x)=Wx 라고 표현함. 이런 경우, cost function도 아래와 같이 조금 더 단순화시켜서 확인할 수 있음.

이 다음, cost(W)는 어떤 방식으로 생긴 것인지 구체적으로 확인해보자. 먼저, W가 1일 경우 cost(W)가 무엇인지 확인해보자. 그다음 W 값에 변화를 주어서 다른 값일 경우도 차례로 확인해보자.

W가 0일 때를 계산해보면, cost(W)는 4.67, W가 1일 때를 계산해보면 cost(W)는 0이 나옴.

위와 같이 W값이 변화함에 따라서 cost(W)의 값들이 각각 계산되어짐. 이 값들을 평면 위에 표현해서 그래프를 그려본다면 어떻게 될까? 그 그래프를 그려봤을 때 아래와 같다.

여기서 우리의 목표는, cost가 최소화되는 점을 찾는 것이었음.

이 최소화된 점을 찾기 위해 사용하는 알고리즘이 Gradient descent algorithm 임. 즉, 경사하강 알고리즘임.
주어진 cost fuction을 최소화하는데 많이 사용되며, cost(W, b)를 최소화하는 W와 b의 값을 찾는데 사용되는 알고리즘임.

이 알고리즘은 아무 점에서나 시작할 수 있음. (0, 0)이나 그 외의 값들 등에서 시작할 수 있는데, W와 b의 값들을 계속해서 변화시킴으로써 cost(W, b)의 값을 최소화시키려고 함. 이 과정을 반복.
이 알고리즘의 장점은, (예외도 간혹 존재하지만) 어느 점에서 시작하든지 간에 항상 최저점에 도달할 수 있다는 것.
이 경사도를 구하기 위해서는 미분을 이용하도록 하겠음.

먼저, 미분을 편리하게 하기 위해 수식을 좀 더 fomal하게 바꾸어주겠음.
시그마 앞에 1/m이 곱해져 있는데, 이를 대신 1/2m으로 바꾸어주겠음.

그 다음, cost(W)값을 미분한 값에 알파 값을 곱한 것을 W에서 빼줌. 이 때 알파 값은 learning rate을 의미함. 여기서 미분한다는 것의 의미는, 해당 점에서의 기울기를 구하는 것과 같다고 이해하기.

위는 미분을 하는 절차인데... 최종적으로 맨 아래의 식으로 도달하는 것을 볼 수 있음. 이 수식을 여러번 실행시키면 W값이 계속해서 변화하는데, 그 값이 바로 처음의 cost minimize하는 방향으로 정해지게 되는 것.
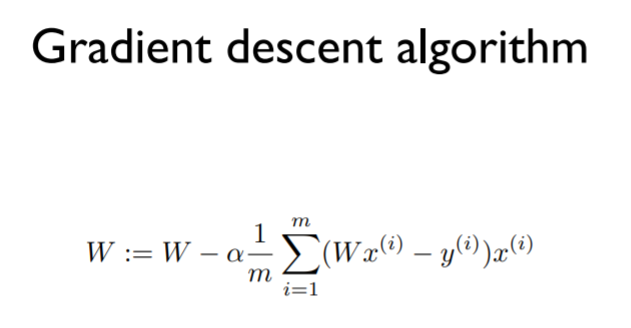
즉, Gradient descent algorighm은 위와 같은 식으로 정리할 수 있다. 이 알고리즘 식을 기계학습에 적용시키면 cost funciton을 최소화하는 W값을 찾아낼 수 있음.

이 때, cost function을 3차원으로 그려본다고 가정하자. 이 때, 바닥면의 가로축을 W, 세로축을 b라고 가정.
문제점이 발생하는데, 각각의 다른 두 지점에서 경사하강 알고리즘에 의해 하강하다보면 서로 다른 두 지점에 도착하게 됨,
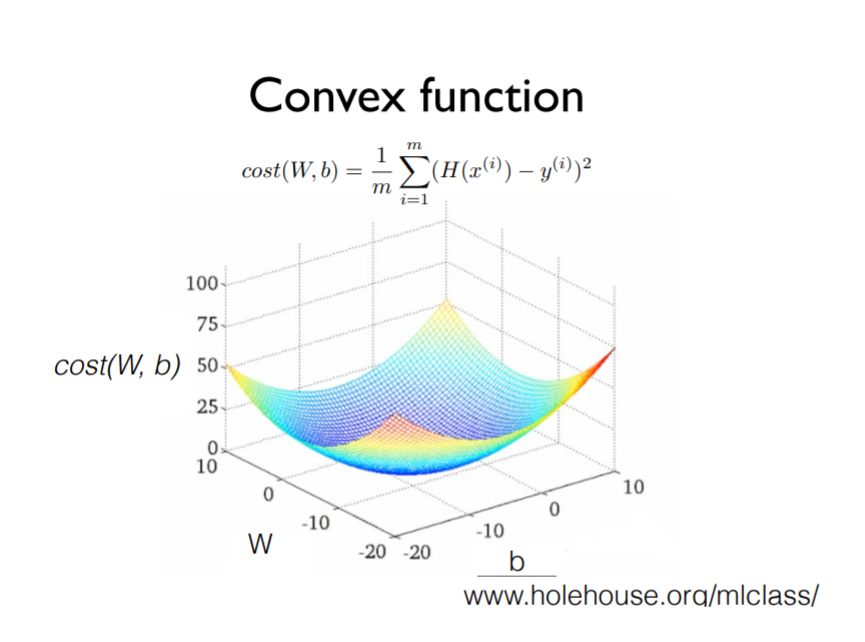
하지만 다행히, 우리의 cost function이나 hypothesis를 가지고 그림을 그릴 때 위와 같이 밥그릇 모양처럼 그래프가 그려지면 어느 점에서 시작을 하더라도 경사하강 알고리즘을 실행하면 같은 점으로 도달하게 됨.
따라서, linear regression의 cost fuction을 설계할 때 위와 같이 convex function의 모양으로 그려지는지 항상 확인해야 함.
'AI > 모두를 위한 딥러닝' 카테고리의 다른 글
| ML lec 5-2 Logistic Regression의 cost 함수 설명 (0) | 2021.05.23 |
|---|---|
| ML lec 5-1: Logistic Classification의 가설 함수 정의 (0) | 2021.05.23 |
| ML lec 04 - multi-variable linear regression (0) | 2021.05.23 |
| ML lec 02 - Linear Regression의 Hypothesis 와 cost 설명 (0) | 2021.05.23 |
| ML lec 01 - 기본적인 Machine Learning 의 용어와 개념 설명 (0) | 2021.05.23 |













