ML lec 5-1: Logistic Classification의 가설 함수 정의
2021. 5. 23. 19:04
출처 : 모두를 위한 머신러닝/딥러닝 https://hunkim.github.io/ml/
모두를 위한 머신러닝/딥러닝 강의
hunkim.github.io

앞선 강의 복습

이전에 배운 regression은 어떤 숫자를 예측하는 것이었음. 이번에 배울 classification은 binary classification이라고도 불리는데, 이는 이름에서 알 수 있듯 2개 중 하나를 고르는 것을 의미함.
이메일의 경우, Spam이냐 아니냐 Facebook의 경우 Show할 것인지 Hide할 것인지 등을 결정.

머신러닝에서는 이렇게 선택 두가지를 0과 1로 나타내기도 함.

그림과 같은 데이터가 있다고 가정해보자.
어떤 학생이 2시간을 공부했을 때는 fail(0)하지만, 일정 시간 이상 공부하면 pass(1)한다는 것을 나타내는 그림임.

앞에서 배운 linear regression을 적용해보면, 이 데이터를 가장 잘 나타내는 linear한 선을 그린 뒤, 이 선을 통과하면 합격, 통과하지 못하면 불합격이라고 표시하면 될 것 같음.
하지만 hours의 값이 커질수록 pass/fail을 결정하는 선이 이동해서 특정 학생의 경우 fail로 오인될 수도 있는 문제가 발생함.

즉, classification에서는 반드시 0과 1의 값만 나타내야 하는데, H(x) = Wx+b의 hypothesis에서는 0보다 훨씬 작거나 1보다 훨씬 큰 값을 나타낼 수도 있게 됨.

따라서 결과값을 0과 1 사이로 압축을 시켜준 다음에 z라는 것을 두고, g(z)라는 함수는 z의 값에 상관없이 0에서 1사이의 값을 반환하는 함수를 찾게 됨.
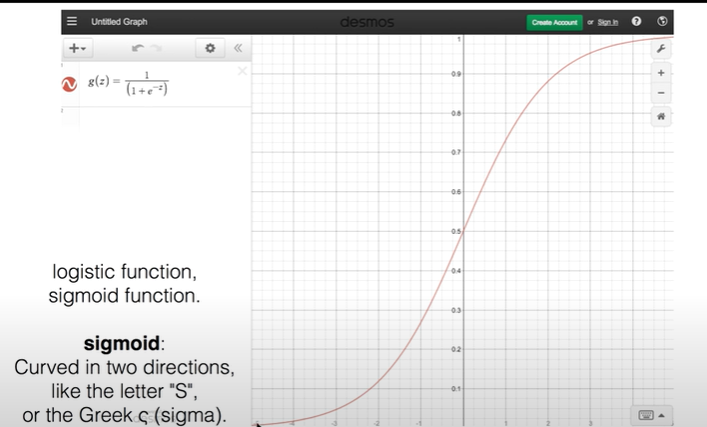
찾게된 함수가 바로 sigmoid 함수임. 이는 logistic function이라고도 부름.
z값이 커질수록 함수 g(z)의 값은 1에 한없이 가까워지며, 1을 넘어가지는 않음.
z값이 작아질수록 함수 g(z)의 값은 0에 한없이 가까워지며, 0 이하로 넘어가지는 않음.
여기서 새로 H(X) = g(z) 라고 정의함.

'AI > 모두를 위한 딥러닝' 카테고리의 다른 글
| ML lec 6-1 - Softmax Regression: 기본 개념 소개 (1) | 2021.05.23 |
|---|---|
| ML lec 5-2 Logistic Regression의 cost 함수 설명 (0) | 2021.05.23 |
| ML lec 04 - multi-variable linear regression (0) | 2021.05.23 |
| ML lec 03 - Linear Regression의 cost 최소화 알고리즘의 원리 설명 (0) | 2021.05.23 |
| ML lec 02 - Linear Regression의 Hypothesis 와 cost 설명 (0) | 2021.05.23 |













